Tanks for the memories

What raffle tickets tell us about the Skripal poisonings

Drawing a raffle

Imagine you are drawing the winning tickets at a raffle where there are 1,000 tickets in the draw. What do you expect to see? Well, obviously it’s very unpredictable - that’s the whole point! Each ticket is equally likely to be drawn out, and we have no way of telling which ones will win. However, in a certain sense, structure will start to emerge out of the randomness.

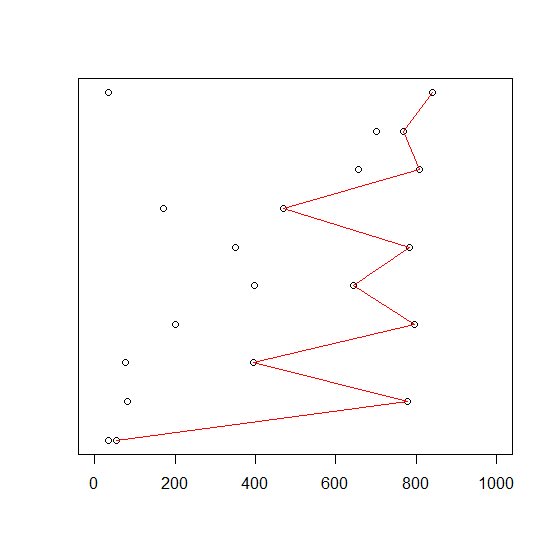
An interesting thing to look at is “what is the biggest number that gets drawn?”. If we draw only two tickets, there’s still not a lot of predictability. I simulated ten examples by computer, with each fake draw being a row of the plot below, in no particular order. You can see that the maximum value drawn out (marked in red for emphasis) is all over the place.

But if I draw twenty tickets then some structure starts to emerge. The maximum value that we see is fairly consistently between about 900 and 1,000. This isn’t a surprise - obviously the maximum can’t be bigger than 1,000 because that’s the largest ticket we put in. But equally for the maximum to be less than 900, we’d have to draw all twenty tickets below that, which happens roughly with probability (900/1000) to the power 20, or 12% of the time.

In fact we can go further: the average of these ten simulated maximums is 949. This is about what you’d expect: with a bit more maths, we know that the average will be about (1000 x 20/21) or 952. (I’m slightly lying here by the way, because I’m glossing over the question of whether you put the raffle tickets back in when you’ve drawn them, but with twenty tickets drawn it won’t make a huge difference).

Even when we drew two numbers, the average of the ten maximums wasn’t crazy - it was 634, not so far from the theoretical (1000 x 2/3) or 667. It’s just that each particular sample could be all over the place.

Turning the tables

Now we can flip the problem on its head. What if we didn’t know how many tickets were in the raffle, and wanted to figure it out from the numbers drawn?

In a sense, this is the difference between probability and statistics. In probability you have a model with fixed values (the number of tickets in the draw) and work out what you expect to see (the biggest value drawn out). In statistics you start with the data you are given (the biggest value seen) and try to work out which values of the model (how many tickets) are consistent with that.

From our examples above, we can see how to guess the number of tickets in this raffle problem. If we know the biggest value drawn, we know there must be at least that many tickets. And our argument with the averages suggests that we could inflate that maximum value by a certain fiddle factor.

For example, when drawing twenty tickets, we’d take our maximum and multiply it by 21/20. In my simulated examples above, this would have given us guesses of 938, 1041, 1035, 961, 1020, 1040, 991, 1004, 1015 and 917 respectively. Not bang on, but not bad!

German tank problem

This all may sound a bit theoretical and pointless, but there’s a really famous example where it all came in handy. This is referred to as the German tank problem, and the Wikipedia page that I just linked to gives an excellent summary.

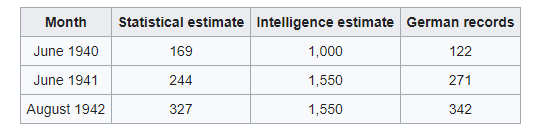
In brief, during the Second World War the Allies needed to estimate the rate of German tank production, to see whether they were blowing up tanks faster than they were being manufactured. One way (“intelligence estimates”) to do this was to use spies, fly over the factories and storage venues, try to crack coded messages and so on.

Another way was to use the kind of statistical analysis that I just described. The Allies had discovered that the gearboxes (and other components) of German tanks were numbered in consecutive order as they were made. This meant that they could find the largest number on a gearbox of a captured tank, inflate it by a fiddle factor, and come up with an estimate of how many tanks had been made.

As the Wikipedia page shows, once records from German factories were recovered at the end of the war, it became clear that the statistical estimates had performed really well - certainly much better than the intelligence estimates.

Djokovic and Skripal

As Wikipedia describes, once these methods had proved their worth in this way, they started to be used in many more contexts - counting other kinds of military equipment in other wars, estimating the numbers of Commodore 64 computers produced and so on.

It’s perhaps surprising that everyone still hasn’t caught on to the implications of this. A couple of more recent examples where consecutive numbering schemes appeared to leak information were:

1. When Bellingcat discovered that the two Russian suspects in the March 2018 Skripal poisonings had passport numbers which only differed by 3 places in the final digits (ending …1294 and …1297). Since this implied that these were fake passports issued in a consecutive block to intelligence agents, it raised the natural question of who had numbers …1295 and …1296 and other passport numbers around that range.

2. When the serial numbers claimed for Novak Djokovic’s positive COVID test in December 2021 appeared to be out of sequence with other tests taken around the same time, drawing into question the exact timings of the tests and threatening his ability to play in the 2022 Australian Open tournament.

Of course, there are countermeasures possible for these methods, but it’s not always as easy as you might think. For example the obvious idea of “just label things with a random number” requires some kind of centralized authority to issue serial numbers or much longer serial numbers, to avoid reusing the numbers - this is due to the birthday paradox.

But overall, it’s fun to see just how far this simple idea of “inflate the maximum” can take us, and I’m sure that it hasn’t been used for the last time.