Why I hate Pi Day

Going round in circles

Today, 14th March, is Pi Day. As a mathematician, I should be happy, but honestly it always annoys me. It’s partly the way that the “3/14” date thing only works in the USA, but there’s more to it than that.

If you are at all science-adjacent, you’re doing incredibly well if you make it through until lunchtime today before someone tells you that this formula is beautiful, and to be honest I don’t really see it.

Fermat's Library @fermatslibrary

Euler's identity displays a profound connection between fundamental numbers π, e (the base of natural logarithms), and i (the imaginary unit). It is considered one of the most beautiful formulas in mathematics.

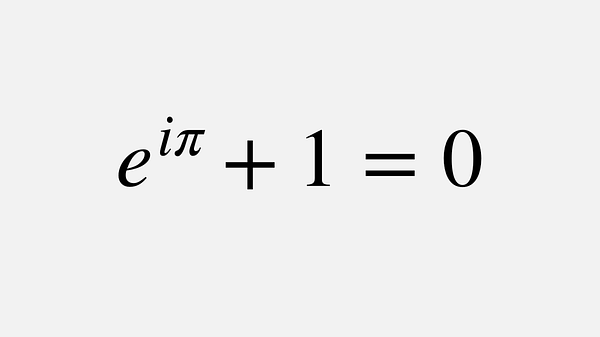
It’s kind of a tautology. It’s like saying that 74 + 4 = 78 — it’s just something that’s true. I think maths can be beautiful, but for me the beauty doesn’t work like this. I find that the true beauty comes through the precise form of a logical argument, the way that all the pieces fit perfectly together and work exactly in the right way like an intricate watch mechanism. If you can find or shape the pieces yourself and put them together in a new way, it’s a wonderful feeling.

But that formula isn’t like this. It’s like a butterfly pinned to a card by a Victorian collector. You can imagine it taking to the air and flying if you think hard enough, but otherwise it just sits and does nothing.

So, what’s it saying, and why does it matter? Well, on some level, it’s just a fancy way of saying that on this graph

when x is equal to π the blue (cosine) curve is at -1, and the yellow (sine) curve is at 0. (Don’t worry if you can’t see why!). Talking about π means that we are measuring angles in radians, but in degrees it is just saying that cos(180)=-1 and sin(180)= 0. The reason for this is that rotating 180 degrees takes us halfway round a circle, and this equation basically says that if you rotate by 180 degrees twice you get back to where you started. Big deal.

Indeed, it’s very often the case that “unexpected” appearances of π in formulas come down to some circle hiding in the argument. For example, the π that crops up in the density of a normal distribution is really because the two-dimensional normal has circular contours. In that sense, π can often be a bit of a disappointment.

So, what can we do with this stuff? One answer is to think about not just the yellow and blue curves above, but whole families of them. We can stretch these curves by whatever amount we like, both horizontally and vertically. If you like, you can think of them as strings on a violin vibrating, to make a note of a particular pitch and volume.

But what’s really cool is that you can build up more or less any curve by adding these particular stretched curves together. You can think of this something like a musical chord: if you play the right combination of notes, you can produce almost any sound you like.

Perhaps most importantly of all, not only can you put these curves together to make a sound, you can use the same ideas to take the recording of a sound and pull it apart to find the individual notes that made it, including one of the most famous chords of them all. That’s real magic. These tricks allow us to find the hidden periodicity in all kinds of places.

This is what’s called Fourier analysis, and the Wikipedia page on the topic gives a small sense of just how incredibly universally useful it is:

Fourier analysis has many scientific applications – in physics, partial differential equations, number theory, combinatorics, signal processing, digital image processing, probability theory, statistics, forensics, option pricing, cryptography, numerical analysis, acoustics, oceanography, sonar, optics, diffraction, geometry, protein structure analysis, and other areas.

It’s the theory that underpins Rosalind Franklin’s Photo 51 - the one that led to the discovery of the structure of DNA. Studying these kinds of harmonics gives insights into fundamental problems in the theory of numbers themselves, and helps understand the structure of the primes¹. Since radio waves take this up-and-down form, every device (whether a phone or an iPad) that connects to a wireless network exploits these ideas of Fourier analysis to make sense of the signals it receives.

But none of this has anything to do with many Pi Day activities. You can memorise as many digits of π or bake as many cookies as you like, but it doesn’t get you any closer to the importance of all this. So sure, π is valuable and maybe even beautiful in a certain light, but I think you need to go one step further under the surface to see why.

And that’s what I’ve been trying to say with Numbercrunch. To sell maths to people as something that’s beautiful feels like preaching to the converted. If you aren’t convinced of the value of the subject then I’m not sure that seeing a few tricks with the digits of π will change your mind. Whereas to feel like maths is not (just) beautiful, but rather is useful and perhaps even necessary as a tool to make sense of the world - that’s a whole other argument, and to my mind a much more convincing one.

1. If you want to read more about how this stuff relates to really deep ideas about numbers (including the most famous unsolved problem of them all), then I can recommend taking a look at the book The Music of the Primes by Marcus du Sautoy.