The Final Cut

Baby I know, the first cut is the deepest

There are some maths topics which always do well on Twitter. Patterns with numbers. Bayes’ Theorem. Exponential growth. Wald’s aeroplane. But that’s just the start.

There’s a mathematical theorem which is so simple that I can explain it to you here, but which wasn’t written down until 1956. Once you get your head around it, you’ll see it everywhere. Like the glasses in cult classic They Live, it can genuinely change the way you look at the world. By seeing how it helps explain NHS congestion, the Ukraine War, energy policy, the vaccine rollout and a lot else besides, you’ll be ready to chew bubblegum and kick ass, metaphorically speaking at least.

And the slogan I want to give you is to focus on your cuts. Let me explain.

Max-flow min-cut

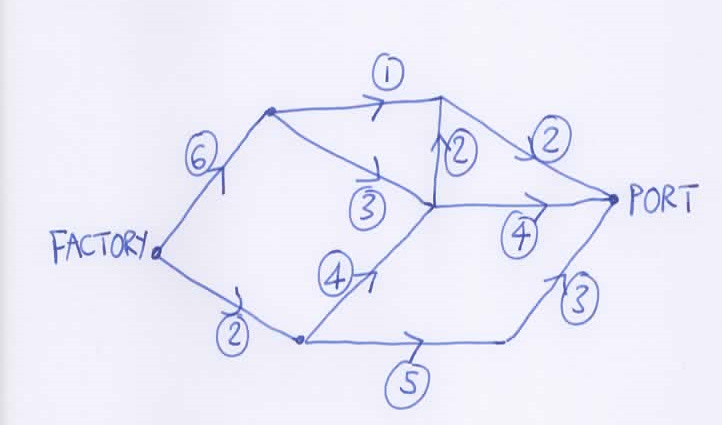
Suppose you own a widget-manufacturing factory. You want to get your widgets to the port. There is a network of (one-way) rail lines, looking like this - the capacity of each line (in trains per hour, say) is marked in a circle. At what rate can we manufacture widgets and get them to the port? (We’ll call this the flow)

As with any maths problem, I recommend that you play around with it yourself first. Have a go at thinking how many widgets you might send down each line.

Hopefully if you do that, you will convince yourself that the answer is a flow of 6 trainloads per hour. This answer comes via the work of Ford and Fulkerson, and is often referred to as max-flow min-cut. The key idea is that of a cut - in the picture below it’s the red line drawn across the network, with the factory on one side and the port on the other. In fact we can think about a cut as defining a set: the set of places on the same side of the line as the factory.

If you add up the ringed numbers on the edges crossing the red cut, you get 6 - and we’ll say 6 is the value of the cut. That tells us that we can’t get a flow of more than 6 widgets/hour through the network as a whole, because every strategy must involve widgets crossing this cut line, and so this cut limits the rate of the whole system.

Using this argument, we know that no flow can be bigger than the value of any cut. And so the maximum possible flow can’t be bigger than the minimum value of the cuts. In fact, it turns out you can’t find a cut with a lower value than 6 (feel free to try!), so this is the minimum value.

In this case then we can’t get a flow bigger than 6. What’s maybe less obvious is that we can achieve a flow of 6. I’ve marked one way of doing this in green - and you’ll notice that all the edges crossing the red cut are at capacity. (There are other ways to route the widgets through the network to achieve a flow of 6, but in each case the edges across the red cut will be at capacity)

In fact, whatever the network looks like, whatever the numbers on the edges, we can always find a flow which hits this target. The maximum possible flow is equal to the minimum value of the cuts. The argument is simple, but I’ll put it in a footnote for people who don’t care about details like this.¹

The implications of this are profound. We can see that it is pointless thinking only about supply and demand without considering the flow through the network and the constraints that this critical red cut puts on it. There would be no point in boosting widget-making capacity or the number of ships in the port, because the network couldn’t cope with that (widgets would pile up in the factory, or ships would sit idle). We need to focus on our cuts.

In lots of ways, this is all obvious, but Ford and Fulkerson only formalised this intuition in 1956. It’s a great example of how maths research is an ongoing thing, and that all the results that matter weren’t invented by the Greeks or Fermat or whoever centuries ago.

Warfare

So far I’ve described a scenario where we have to do our best with a network that’s given to us. But in the real world we aren’t just passive observers, we can affect the network itself. And the joy of the max-flow min-cut theorem is that it tells you how to do this.

I’ll talk later about some examples where we might try to build capacity, to improve the value of the flow by adding more links across the critical cut. However, we can also think of the situation the other way around, where we seek to lower the flow by reducing the value of the critical cut.

I recently wrote about 617 Squadron, and their attempts to destroy strategic infrastructure in the Second World War. You can think of that in precisely these terms: by targetting bottlenecks in the transport network, you can degrade the whole system. By bombing the Bielefeld viaduct or the Saumur tunnel, the flow of German troops and supplies to the front was seriously disrupted, and the minimal cut degraded.

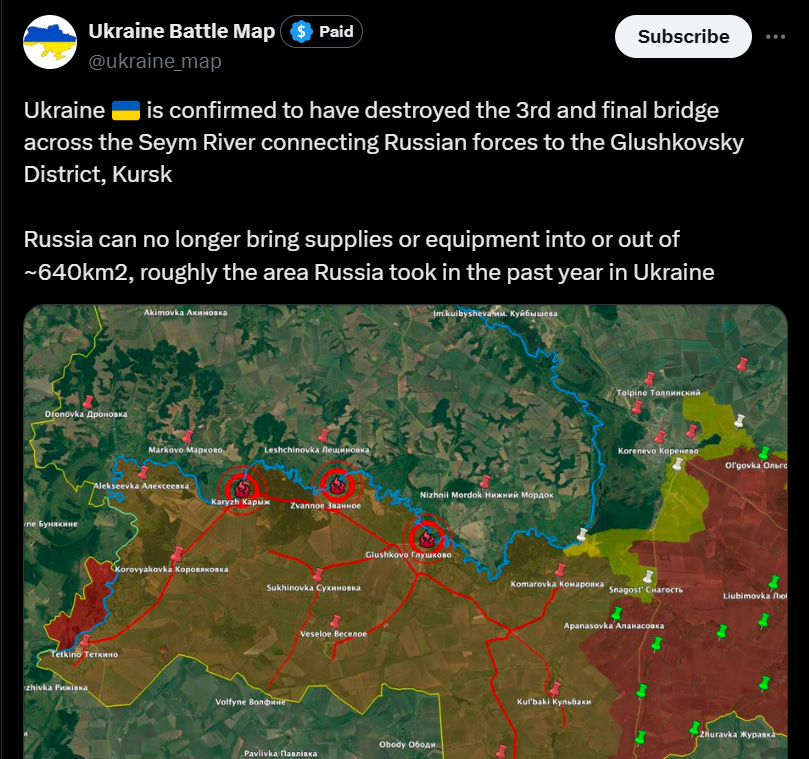
You can see it even more starkly in the Ukraine War, where the cut can be already on the ground in the form of a river. By identifying that geographical constraint, and destroying the bridges across it, Ukraine managed to seriously inhibit flows of Russian supplies into the territory they seized in Kursk in the summer and are so far managing to hold.

Indeed, many forms of warfare, whether open or covert, can be seen in these mathematical terms. By cutting submarine internet cables, blowing up the Nordstream pipeline or attacking the Kerch Bridge, each side has identified critical cuts, and understood that targetting them will have a much greater effect on the flow of resources than indiscriminately bombing in general.

Building the grid

We can also think in terms of max-flow and min-cut when understanding the challenges of decarbonising the electricity grid. Here the situation is more complicated, because there isn’t a single source of energy trying to supply a single place where it is consumed.

Instead, we need a grid robust enough to link multiple power stations, wind and solar farms to homes, factories and shops, bearing in mind that supply and demand will vary by the minute, the day and the season, and that links may sometimes go down for maintenance or because of bad weather. However, many of the max-flow min-cut principles do still apply.

UK National Grid map, taken from https://www.nationalgrid.com/electricity-transmission/network-and-infrastructure/network-route-maps

Fundamentally, there’s no point in building too much wind and hydro generating capacity in Scotland, if the majority of the UK’s demand is in England and there aren’t high enough capacity links between the two. Indeed you can see this problem very clearly on the UK National Grid map: there’s a pretty clear cut more or less along the line of the England-Scotland border, and so the constraints on the two cables crossing that border govern how much electricity can flow from North to South.

Of course, the National Grid are aware of this, and are looking to rectify the problem. There are plans afoot to boost the flow across this cut by building a new undersea cable. But that’s not going to happen overnight, and in the meantime the lack of realistic storage capacity means that very often Scottish windfarms are being paid for energy which can’t be usefully used, with the problem only getting worse as more generation capacity comes online.

NHS capacity

We can think about the operation of systems like the NHS in a similar way. The previous examples involved some physical network (of train tracks, roads or wires) existing in space. However, we can abstract this into a more mathematical idea of a virtual network, one that doesn’t necessarily have a physical manifestation, but that we can try to optimise in the same way.

For example, we can think about patients flowing through a network, where each edge represents some form of intervention (booking an appointment, seeing a doctor, getting treated). We’d like to make sure that as many people as possible receive a successful outcome, and efficiently navigate through this network.

This is a bewildering problem, but the same principles apply. Imagine that for a particular form of cancer, there is a flow from screening, to needing a preliminary biopsy, to processing that in the lab, to performing an operation if necessary. We need to know where the bottleneck is, in order to focus on the right cut. You could easily imagine a situation where politicians announce boosts in funding for screening or operations, which would have no effect on the overall efficiency of the system if the critical constraint is the amount of lab capacity for example.

In some ways it’s encouraging: if we can identify the real constraints then we just need to optimise those, rather than having to increase funding across the board.

Tim Leunig

has been thinking about some of these on his Substack lately: do we need trained doctors to explain procedures and ask patients to get ready or can someone else do it? Can we have a standby waiting list to balance out missed appointments? It would be nice to think that this kind of system-level thinking could be put place right across the board.

Project management

Indeed, it feels to me that everyone in managerial or leadership roles should understand their organisation well enough to know where the critical cut is that’s preventing it from being more productive. Which members of the team are most under pressure? Which resources form the overall constraint? By knowing this and targetting improvements in the right place, by focusing on the cut, the efficiency of the whole system can be boosted in the most telling way.

Reading the Kate Bingham book, it’s striking that much of the success of the Vaccine Taskforce came from thinking in this way. By investing in a range of possible vaccines, there were multiple routes through the uncertain clinical trials process which could deliver success. But Bingham and her team were thinking about much more than simply the vaccines themselves. She describes confirming

we have got 150 million vials, stoppers and overseals … Do we have enough tubular glass to make the vials and do we have enough of the borate silicate sand to make tubular glass?

Every step of the process was considered and optimised, from rehearsing carrying vaccines around using pizza boxes to investing in a new type of syringe and training vaccinators even before the vaccines were ready.

By thinking ahead, by identifying each of these possible constraints and thinking how they could be overcome, a huge range of possible cuts were improved, allowing for the successful flow of patients through the vaccination system in due course. If any one of them had gone wrong or not even been considered, the whole system could have run far less smoothly.

Of course most of us will never have to manage a system as complicated as the Vaccine Task Force did, but nonetheless the same mathematical principles apply. Even in everyday life, we should all be focusing on our cuts, and looking for ways to do better.

1. Suppose we have the best possible flow. Think about the set of places in the network to which we can increase the flow of widgets.

a) All the edges leaving that set must be at capacity (or the set would be bigger than it is)

b) The factory is in this set, the port isn’t (or the flow wouldn’t be optimal), so this choice of set gives us a cut.

Putting a) and b) together, we can see that this flow is equal to the value of the corresponding cut. That tells us that this must be the minimum cut value (there can’t be a better cut elsewhere, because it would be lower than the value of the flow), and we are done.