Playing party games

Don't follow leaders, watch the parking meters

How many parties are there in UK politics? Obviously it depends how you count, how far you go down the list, whether you include the Scottish Libertarian Party and so on. But I want to argue that the answer at the moment is effectively about 5.6, and that’s more than we’ve ever had.

To explain what I mean, look at this opinion poll, which is fairly representative of current British politics. There are six parties listed, but some of them don’t stand much of a chance. So how to count?

In fact, if you’re good at mental arithmetic, you’ll notice that there’s 4% missing, so we’ll lump that together and call it The Rest. But that doesn’t really help.

Luckily, there’s a mathematical answer, going back to the work of the great Claude Shannon. Shannon was the inventor of Information Theory, which is really my day job - I have “Information Theory” in my job title, and publish research in the area¹. One of the first posts I wrote on Substack was an introduction to some of Shannon’s work, and the key was that Shannon:

introduces the idea of a source of randomness, and mentions the idea that some sources are more random than others, and that this is somehow to do with predictability

Shannon introduced entropy, as a numerical measure of randomness. There’s a fun story that the name came from von Neumann:

You should call it entropy for two reasons: first because that is what the formula is in statistical mechanics but second and more important, as nobody knows what entropy is, whenever you use the term you will always be at an advantage!

though there’s a good chance that it might not be true (I guess

Ananyo Bhattacharya

of this parish may know - either way, you should read his book and subscribe to his Substack!).

Anyway, what really matters is that Shannon gave us a way to quantify that some sets of probabilities (like the opinion poll chances above) are more random than others. His real insight was that this has to do with predictability, and how efficiently we can describe the likely outcomes in binary code. I don’t want to get into lots of equations, but there are two things you need to know:

1. Where all the probabilities are all equal, the entropy takes a nice value.

2. We can work out the entropy even when the probabilities aren’t all equal.

To explain the first one at least, if we have some experiment which is equally likely to give us each of n values, then Shannon’s entropy formula just gives us the logarithm of n. For example, if we toss a coin (2 values), the entropy is the logarithm of 2. If we roll a standard die (6 values), the entropy is the logarithm of 6. If we roll a fancy 20-sided die, the entropy is the logarithm of 20.²

This gives us a way to calibrate uncertainty. The more equal the probabilities, the bigger the entropy. But if we have a different set of probabilities with entropy equal to the logarithm of 6, we can say that the outcome is as unpredictable as rolling a 6 sided die. In mathematical language, we need to invert the logarithm function³. In general, if the entropy is H, then the exponential

\(2^H\)

gives us the “effective number of outcomes” - a comparator for how unpredictable things are.

This is maybe a bit mind boggling, so we should go back to opinion polls. If we have a poll which is a four way tie 25-25-25-25, then picking out a voter at random from the population is like rolling a four-sided die. The entropy would be the logarithm of 4 and the effective number of outcomes would be 4. And in general we can talk about the effective number of parties: if you give me the percentages, I can tell you the entropy, and we can take the exponential.

For the numbers we started with, it turns out that the entropy is about 2.48, and so the effective number of parties is 5.6. If I choose a random member of the public and want to know who they’ll vote for, it’s a bit more predictable than rolling a dice, but only just.

Now, the nice thing is that we can see how this has changed over time. I can pull out the vote shares of every UK general election for 100 years, calculate the entropy⁴ and hence find the effective number of parties, and it looks like this:

What you’ll notice is that we spent most of the time from 1920 to 1980 or so wiggling around somewhere between two- and three-party politics. The Liberal party came and went, there was a national government in the 1930s and so on, but we were generally in that range.

From the 1980s onwards, we were on a slow climb into three-and-a-bit party politics, as the rise of the SDP, Paddy Ashdown, Cleggmania and all the rest of it took us into the world of a viable third party. After that, things got a bit weird: the rise of the Brexit Party in 2015 took us into the world of four-party politics, before the two Brexit-dominated elections of 2017 and 2019 turned into more of a straight two-party fight.

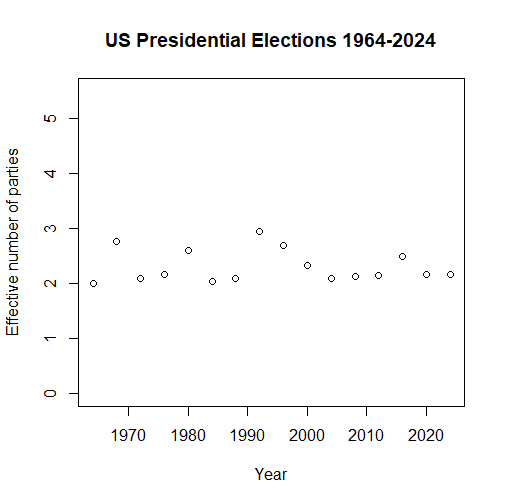
But then, in 2024, with Reform, the Greens and so on, we were up into the world of five or more party politics - and the effect has only continued to grow. So if you feel as if the UK electorate has never been so fragmented, then at least there’s some solid mathematical justification for that. In contrast, American politics has been much more sedate:

Most of the time it’s been pretty much a straight two-party fight, except for the odd disruptor (George Wallace in 1968, John B. Anderson in 1980, Ross Perot in 1992 and 1996) turning it into something more like a genuine three-way race. Because the graph of the entropy function is reasonably flat close to 50% splits, even Nixon’s stonking 60% vote share in 1972 doesn’t take us much below two parties.

Interestingly, because entropy only depends on probabilities and not labels, the recent swings in party from Obama-Trump-Biden-Trump hardly show up on the graph (because there have been relatively small shifts in vote share).

It’s maybe nothing we didn’t know already, but it’s a fun toy to play with nonetheless. It's nice to somehow quantify the idea that Russia has moved towards autocracy from Putin’s first win in an election with an effective 3.6 parties to his latest one with 1.6. Even that’s a long way from the 1994 Turkmenistan referendum with its effective number of outcomes being 1.001, in stark contrast to the 2022 French presidential election with an effective 6.8 candidates.

But I think there are a couple of serious lessons for us. Firstly, in the UK setting I’ve only focused on inputs (votes) and not on outputs (seats). I don’t want to get into an argument about the First Past The Post system, but it won’t have escaped Labour’s notice that their landslide majority was built on a very divided electorate. While in 2024 there was an overwhelming mood of “get the Tories out”, that feels unlikely to be such a strong motivation in 2029 when Labour will have to run for re-election based on their record.

Secondly, this fragmentation of the electorate makes the job of modellers and pollsters much harder. As I pointed out in 2022, the wide range of experiences of COVID infection and vaccination by then meant that we could no longer apply simple models that put people into a few categories. Similarly, now we are far away from two party politics, the classic Swingometer is no longer really a valid tool.

Since we need to track voters for perhaps six parties, there are fifteen different movements between pairs of parties to study, rather than just looking at overall headline vote shares. Since so many constituencies have their own local dynamics and different populations of voters, it may matter a lot whether there is a small Labour to Green swing or a Conservative to Reform one for example, and a traditional opinion poll with its wide margin of errors may not pick that up. It’s very much at that stage where more sophisticated modelling methods such as MRP might be required (even if many of these were quite inaccurate in predicting the 2024 election).

Overall then, at least as long as we remain in this high entropy world, politics has the potential to be very volatile for the next few years, and the pollsters and opinion columnists will definitely have to earn their money.

1. Or I try to, when I get time these days

2. In fact, you don’t really need Shannon for this part. This is the argument of Hartley from 1928, twenty years before Shannon’s masterwork. Ecclesiastes 1:9 and all that.

3. I didn’t get into this, but we generally use base 2 logarithms, to make the unit of entropy the “bit” (in the sense of binary 0-1 digits).

4. I cheated, and lumped together all the parties below 5% as “The Rest”